دانلود اپلیکیشن
در این درس حالت های مختلف هم نهشتی مثلث ها را بررسی می کنیم و در نهایت حالت های هم نهشتی مخصوص مثلث های قائم الزاویه را توضیح می دهیم …
حالت های هم نهشتی مثلث ها
به دو مثلث زیر توجه کنید.
مثلث ABC با یک تقارن نسبت به خط چین برروی مثلث EFG منطبق می شود.
ضلع ها و زاویه هایی که روی هم منطبق می شوند را متناظر می گویند.
مثلا زاویه A و G و ضلع های AB و EG باهم متناظرند.
در ریاضی هشتم از ما می خواهند هم نهشت بودن دومثلث را ثابت کنیم.
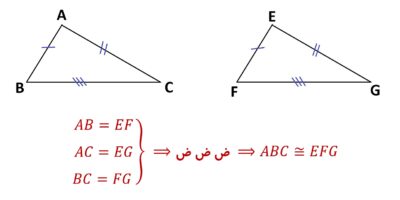
در حالت کلی اگر یکی از سه شرط زیر برقرار باشد، دو مثلث هم نهشت هستند.
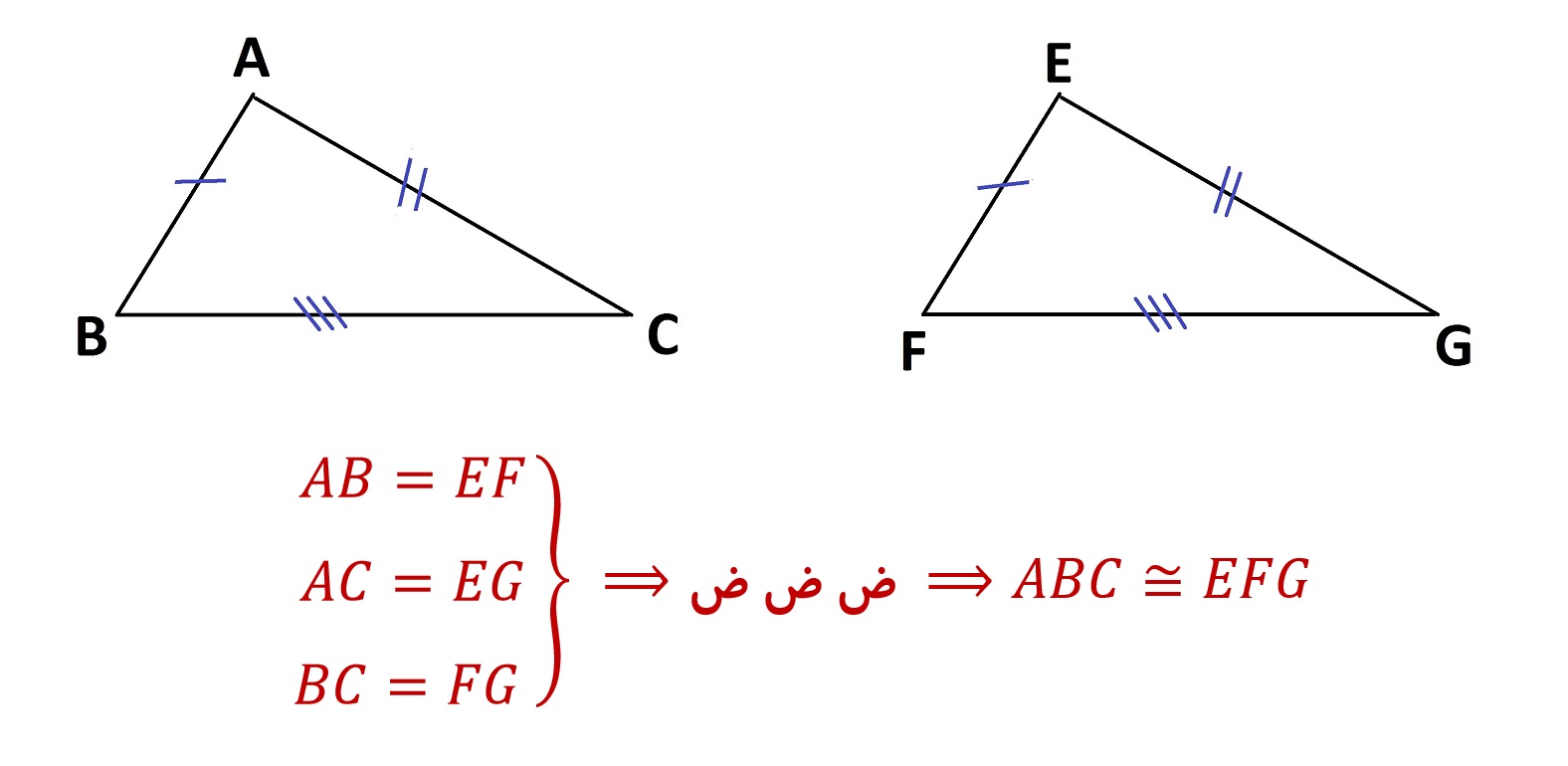
- هر سه ضلع یک مثلث با هر سه ضلع مثلث دیگر مساوی باشد. (ض ض ض)
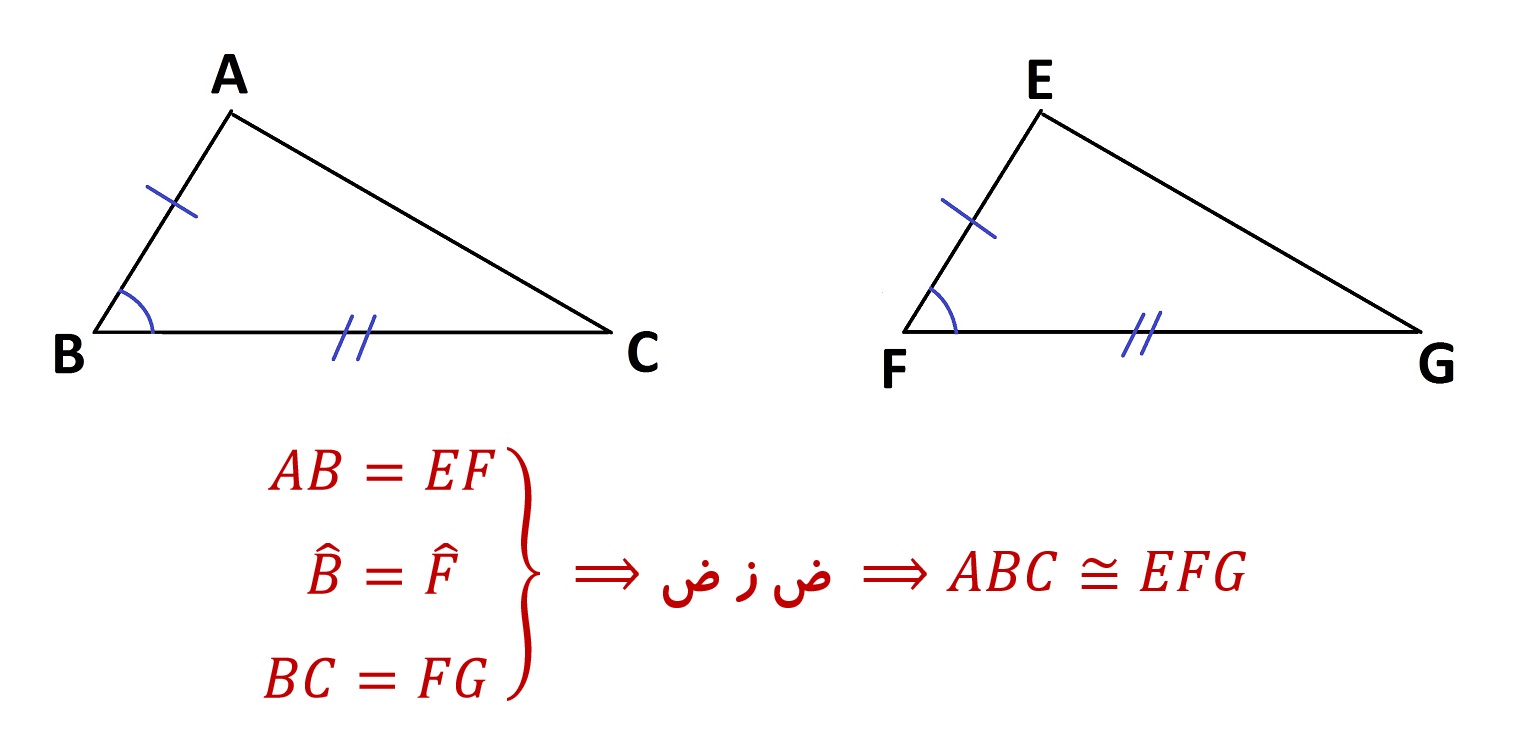
- دو ضلع و زاویه بین آن ها از یک مثلث با دو ضلع و زاویه بین آن ها از مثلثی دیگر مساوی باشد. (ض ز ض)
- دو زاویه و ضلع بین آن ها از یک مثلث با دو زاویه و ضلع بین آن ها از مثلثی دیگر مساوی باشد. (ز ض ز)
مثال برای حالت اول :
مثال برای حالت دوم :
مثال برای حالت سوم:
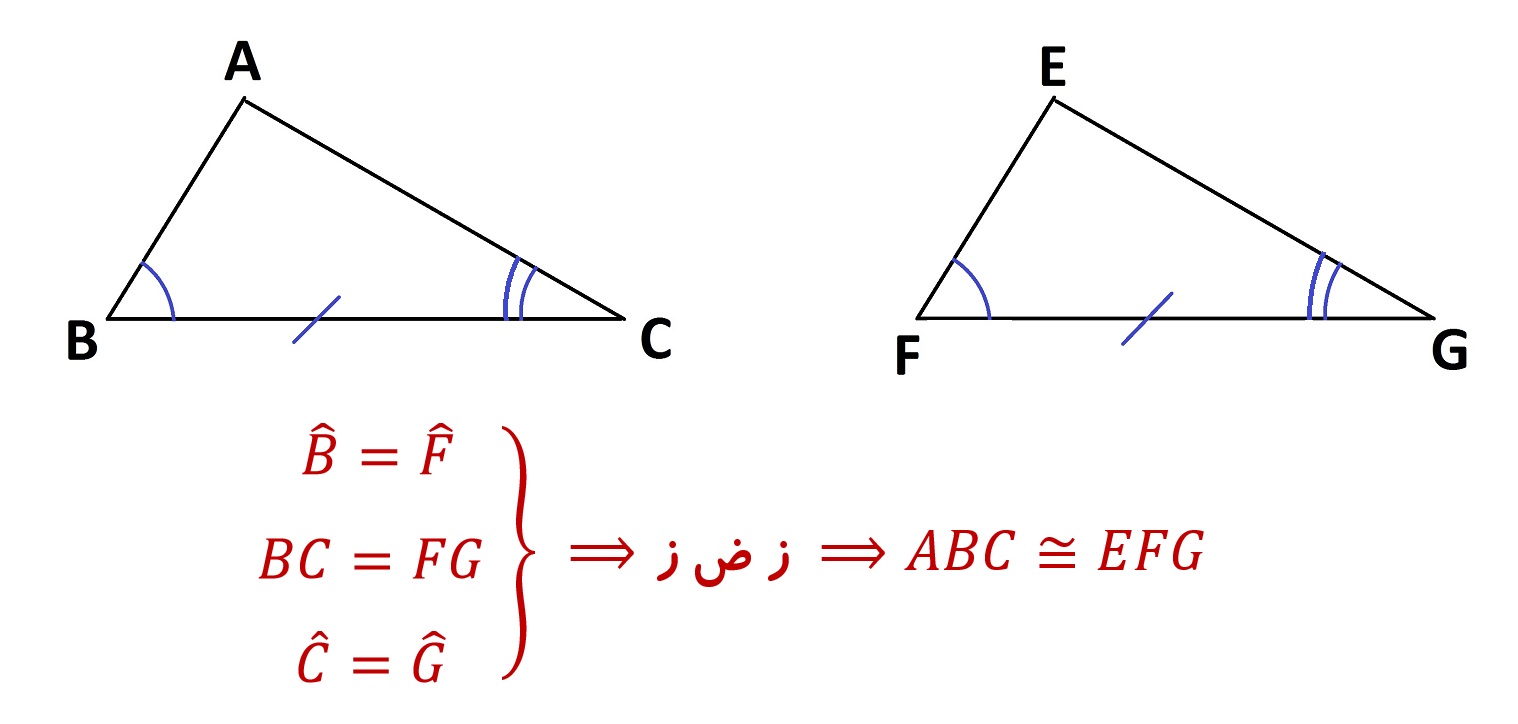
تذکر: درحالت (ض ز ض) ابتدا دو ضلع مساوی را پیدا میکنم. در صورتی که زاویه بین آن ها در دو مثلث مساوی باشد، هم نهشت خواهند بود. مثلا در شکل زیر دو مثلث هم نهشت نیستند.
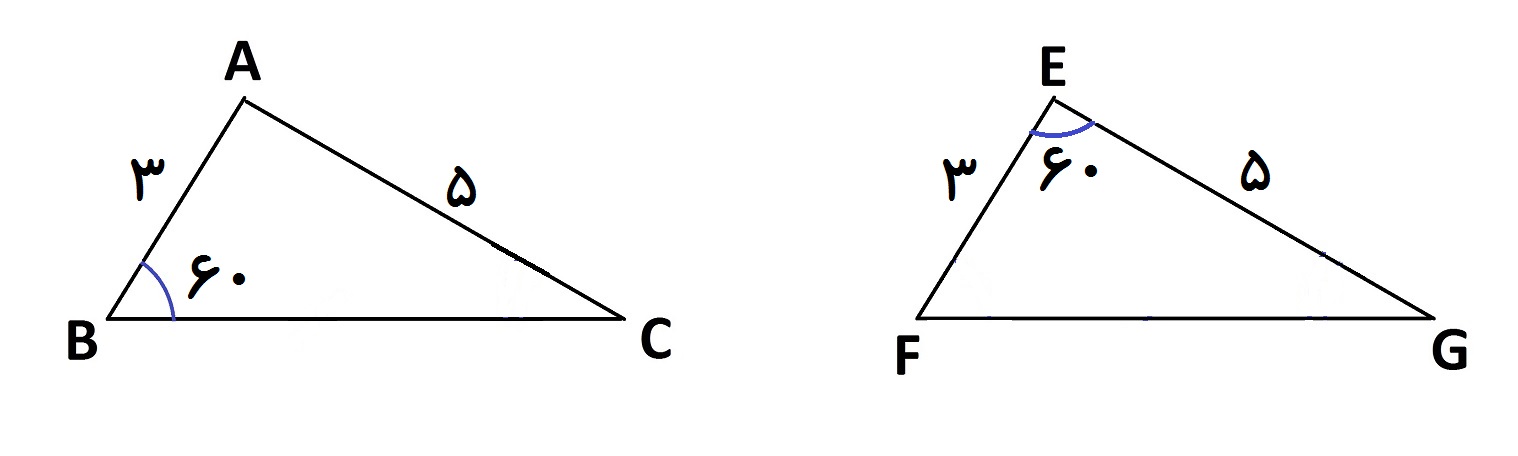
چون زاویه بین دوضلع مساوی ، زاویه های A و E هستند و این دو زاویه باید مساوی باشند نه اینکه زاویه B و E
تذکر: در حالت (ز ض ز) نیز همانند بالا ابتدا دو زاویه مساوی را پیدا می کنیم در صورتی که ضلع بین آنها در دو مثلث مساوی باشد، مثلث ها هم نهشت خواهند بود. مثلا در شکل زیر دو مثلث هم نهشت نیستند
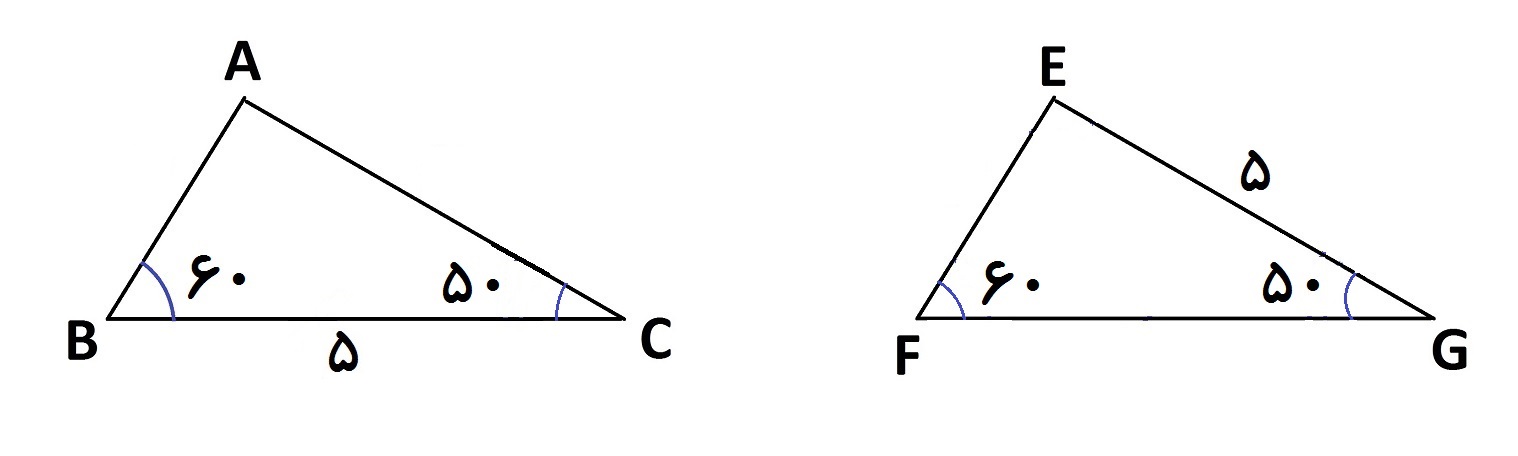
چون ضلع بین دو زاویه مساوی، ضلع های BC و FG است و این دو ضلع باید مساوی باشند نه اینکه ضلع BC و EG
هم نهشتی مثلث های قائم الزاویه
در مثلث های قائم الزاویه، مانند سایر مثلث ها اگر هر یک از شرایط (ض ض ض) یا (ض ز ض) یا (ز ض ز) رخ دهد، دو مثلث هم نهشت خواهند بود. به طور مثال در شکل زیر، این دو مثلث بنابه حالت (دو ضلع و زاویه بین) هم نهشت هستند.
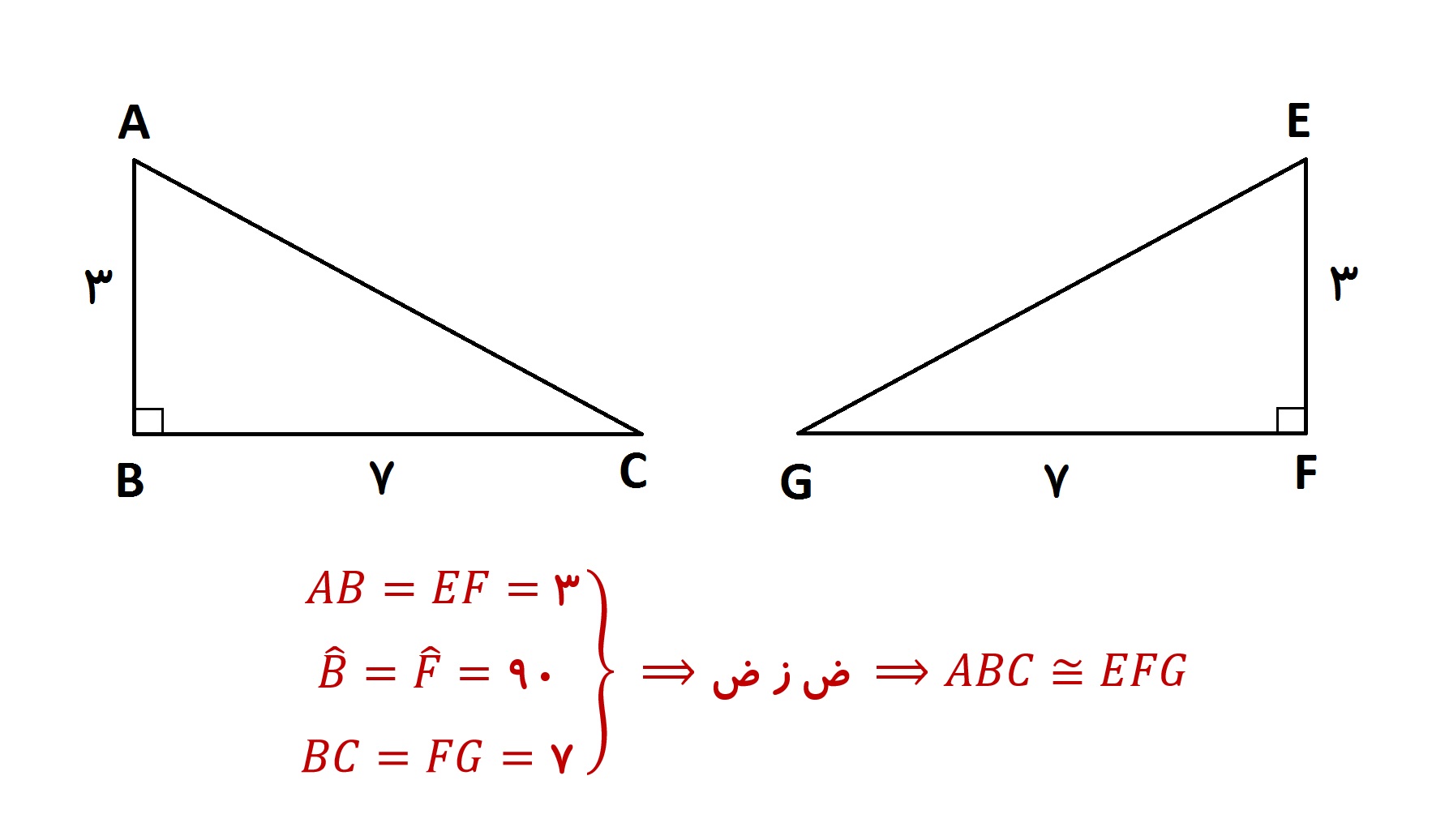
اما باید این نکته جدید رو یاد بگیریم که:
اگر در دو مثلث قائم الزاویه وتر ها باهم مساوی باشند برای هم نهشت بودن آنها فقط کافیه یک ضلع (غیراز وتر) و یا یک زاویه (غیر از ۹۰ درجه) باهم مساوی باشد. بنابراین می توان گفت دو مثلث قائم الزاویه هم نهشت هستند، اگر :
- وتر و یک ضلع از یک مثلث با وتر و یک ضلع از مثلث دیگر مساوی باشد. (و ض)
- اگر وتر و یک زاویه از یک مثلث با وتر و یک زاویه از مثلثی دیگر مساوی باشد. (و ز)
مثل برای حالت اول:
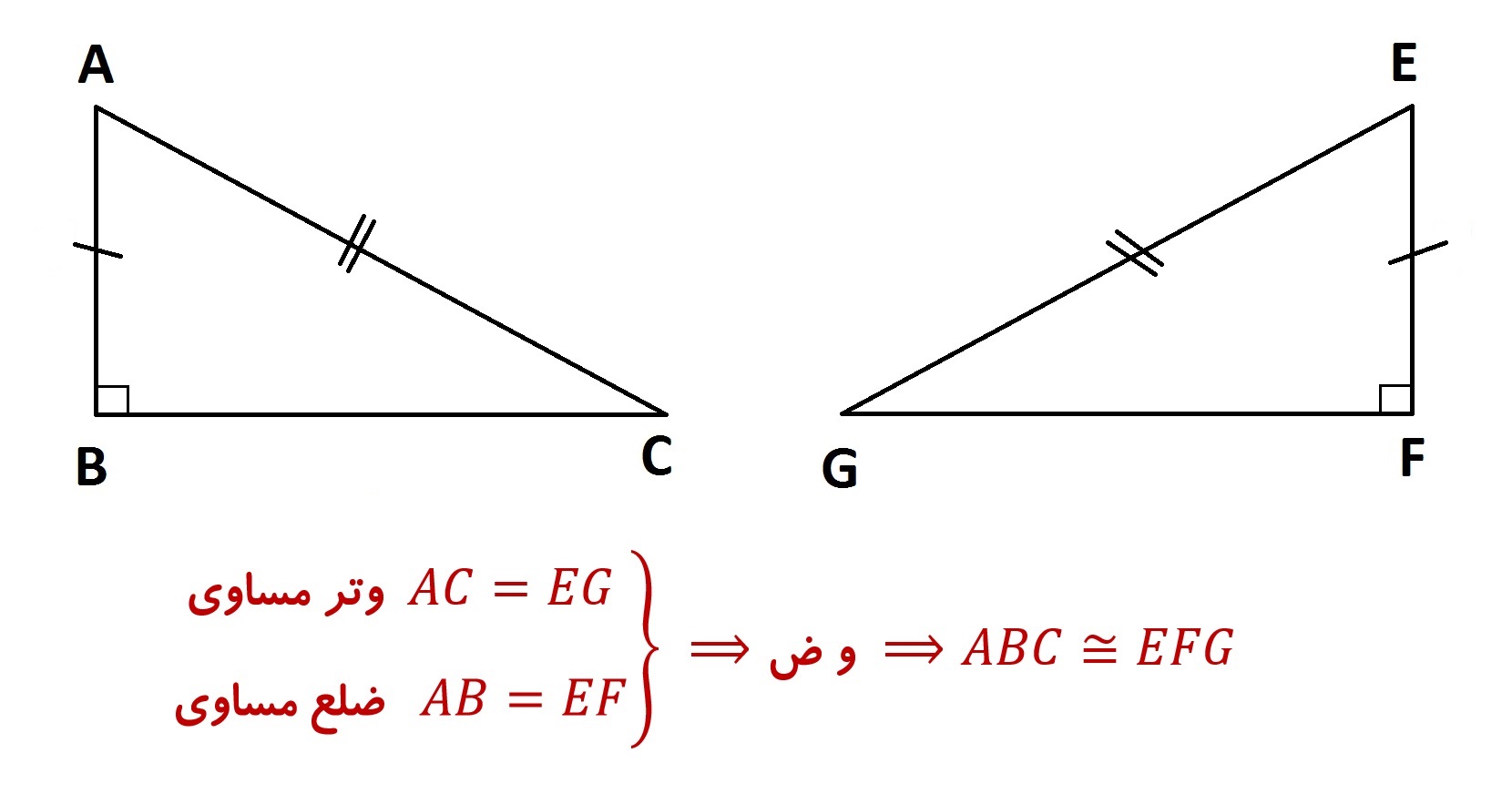
مثال برای حالت دوم:
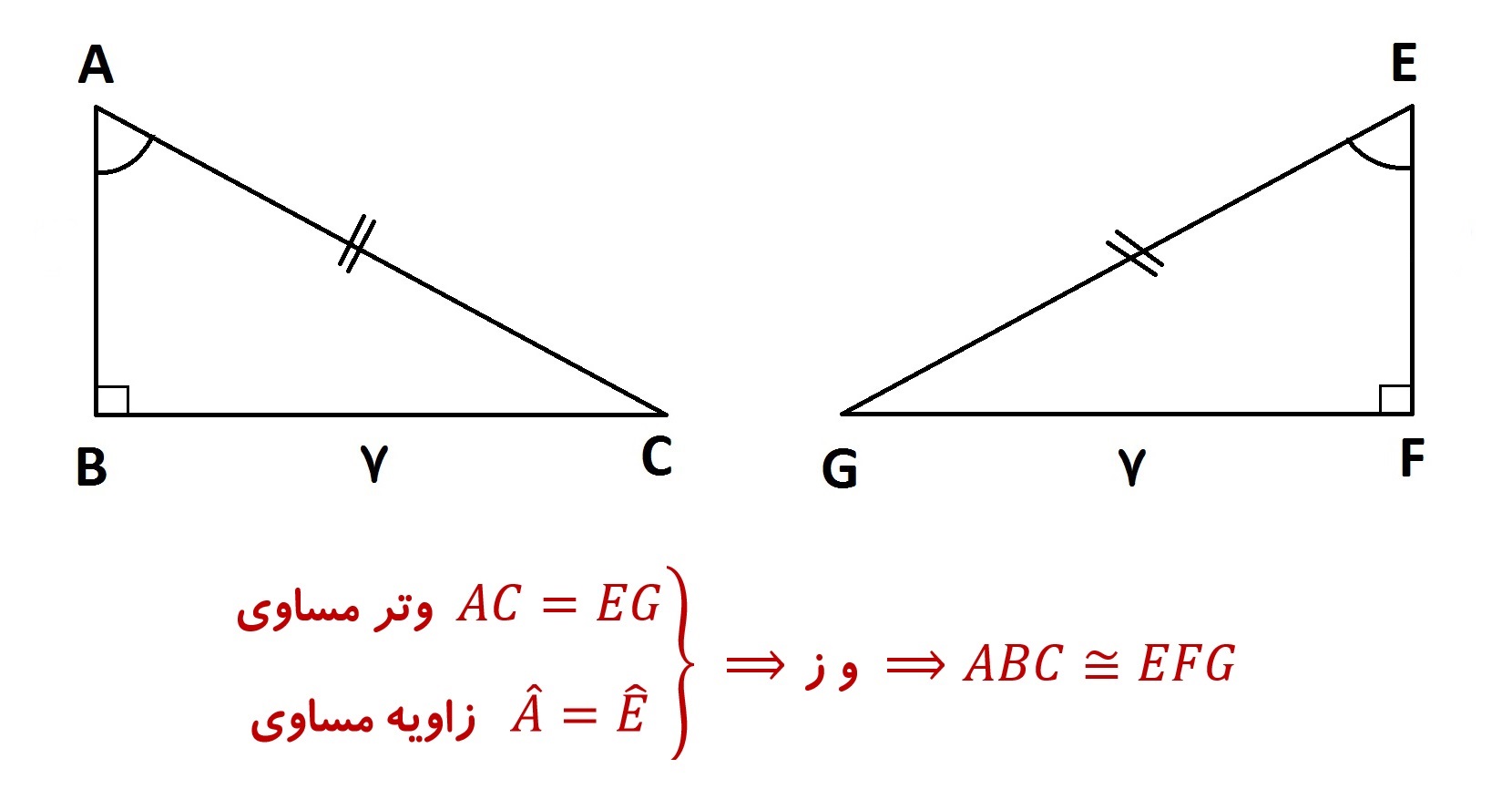
- رابطه فیثاغورس در مثلث قائم الزاویه و طریقه استفاده از آن
- شکل های هم نهشت و روش محاسبه مجهول در ضلع یا زاویه
- آزمون فصل پنجم ریاضی هشتم بردار و مختصات با پاسخ تشریحی
- حل معادله برداری به روش مختصاتی و پیدا کردن بردار مجهول
- جمع ترسیمی بردار ها در صفحه شطرنجی و محاسبات مختصاتی آنها
- تجزیه بردار بر روی دو راستای دلخواه به کمک رسم خطوط موازی
- مختصات بردار با طول و عرض و بردارهای واحد مختصاتی
- ضرب عدد در بردار به صورت ترسیمی و مختصاتی
سلام میتونم از مطالب تون استفاده کنم وبا این مطالب پاورپوینت درسی درست کنم؟؟؟؟
چطور میتوان فهمید که اطلاعات برای پیدا کردن هم نهشتی کافی نیست
اگه اطلاعات مسئله شما برای هیچ کدوم از حالت های گفته شده در این مطلب مناسب نباشه، یعنی اطلاعات کافی نیست. مثلا برای دو مثلث عادی، ممکنه برابری دو ضلع و یک زاویه را داشته باشیم، اما اون زاویه ، دقیقا بین دو ضلع قرار نداشته باشه. بنابراین نمی توان از حالت (ض ز ض) استفاده کرد.