دوتا از نماد های مهمی که در بحث مجموعه ها استفاده میشه نماد عضو بودن در مجموعه و زیرمجموعه بودن هست. این دو نماد باهم تفاوت بسیاری دارند که الان میخوایم با همدیگه یاد بگیریم. اگه این نکته امروز رو یاد بگیرید مطمئن باشید …
دوتا از نماد های مهمی که در بحث مجموعه ها استفاده میشه ،نماد عضو بودن در مجموعه و زیرمجموعه بودن هست. این دو نماد باهم تفاوت بسیاری دارند که الان میخوایم با همدیگه یاد بگیریم. اگه این نکته امروز رو یاد بگیرید مطمئن باشید ازین به بعد به راحتی همه سوالای صحیح و غلط در این مورد باهاش رو به رو بشید، رو میتونید به آسونی جواب بدید.
عضو بودن در مجموعه
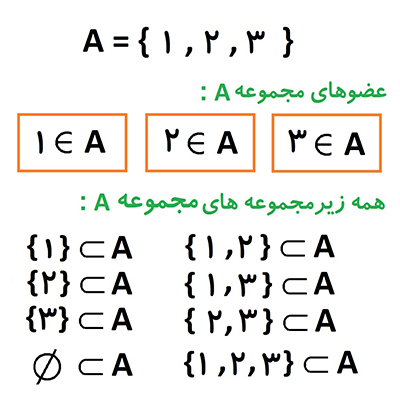
به طور مثال مجموعه { ۳ و ۲ و ۱ }= A رو در نظر بگیرید. این مجموعه همونطور که ملاحظه میکنید ۳ تا عضو داره که این مطلب رو به صورت زیر نشون میدیم:
| ۳ ∈ A | ۲ ∈ A | ۱ ∈ A |
البته اگه دوتا از عضو ها یا بیشتر رو بخوایم، باهم دیگه و به صورت خلاصه بگیم که عضو A هستن، میتونیم از شیوه های زیر استفاده کنیم:
۱ , ۲ ∈ A
۱ , ۳ ∈ A
۲ , ۳ ∈ A
۱ , ۲ , ۳ ∈ A
این که از کدوم مدل بخایم استفاده کنیم، کاملا بستگی به صورت سوالمون داره. البته معمولا صورت سوال خودش اینا رو مینویسه و فقط از ما درست یا غلطیش رو میپرسه.
حالا اگه یه چیزی عضو مجموعه نباشه ، اون رو باید چطوری نمایش بدیم؟ مثلا در مجموعه بالا میخوایم بگیم که عدد ۲ عضو این مجموعه نیست. باید بنویسم:
۲ ∉ A
بیاین یه مثال در این مورد رو باهم کار کنیم.
مثال : باتوجه به مجموعه { ۱۲- و Φ و ۸- و a و ۵ و ۶ } =A به درست یا نادرست بودن عبارات زیر رو مشخص کنید.
| -۱۲ ∉ A | a , -8 ∈ A |
| Φ ∈ A | ۵ , ۶ , ۷ ∈ A |
جواب : به صورت خلاصه جواب میدم ، توضیح اگه نیاز بود توی کامنت بپرسید لطفا
| صحیح | a , -8 ∈ A |
| غلط | -۱۲ ∉ A |
| غلط | ۵ , ۶ , ۷ ∈ A |
| صحیح | Φ ∈ A |
پیشنهاد می کنم درس زیر رو مطالعه کنید :
تعریف مجموعه ها رو با نوشتن اعضا ، نمودار ون و نماد ریاضی یاد بگیریم
تعریف زیرمجموعه و نماد آن
اگه از یک مجموعه ، یک یا چندتا عضوش رو انتخاب کنیم و اونا رو درکنارهم داخل یک آکولاد { } قرار بدیم، میگیم که ما یک زیرمجموعه از مجموعه اولی تشکلیل دادیم. مهم ترین چیزی که اینجا باید رعایت کنیم همون علامت آکولاد هستش. اگه آکولاد نذاریم میشه مثل چیزایی که واسه عضویت نوشته بودیم و دیگه زیرمجموعه به حساب نمیاد.
دوباره مجموعه { ۳ و ۲ و ۱ }= A رو در نظر بگیرد. همون چیزایی که واسه قسمت عضویت نوشته بودیم رو اگه الان اینجا دوباره بنویسیم و البته داخل یه آکولاد بنویسیم. علامت عضویت رو باید برداریم و بجاش علامت زیر مجموعه بودن رو قرار بدیم، یعنی :
{ ۱ } ⊂ A
{ ۲ } ⊂ A
{ ۳ } ⊂ A
{ ۱ , ۲ } ⊂ A
{ ۱ , ۳ } ⊂ A
{ ۲ , ۳ } ⊂ A
{ ۱ , ۲ , ۳ } ⊂ A
خب حالا بذارید یه نکته مهم رو براتون بگم. مجموعه تهی رو که یادتون هست !؟ اگه یادتون باشه به مجموعه ای که هیچ عضوی نداشته باشه، میگم مجموعه تهی و اون رو با نماد Φ و یا { } نمایش میدن. حالا نکته چیه !؟
نکته : مجموعه تهی زیرمجموعه همه مجموعه ها هست.
پس علاوه بر اون ۷ تا زیر تا مجموعه که بالا نوشتم باید به آخرشون این رو هم اضافه کنیم:
{ } ⊂ A یا Φ ⊂ A
فرمول تعداد کل زیرمجموعه های یک مجموعه n عضوی
دیدم برای یک مجموعه که سه تا عضو داره ، ما میتونیم ۸ تا زیر مجموعه بنویسیم. به نظر میرسه باید یه فرمولی وجود داشته باشه که بشه تعداد زیرمجموعه هایی که میشه نوشت رو از همون اون محاسبه کرد. فرمولش رو در زیر باهم میخونیم :

برای بدست آوردن تعداد زیرمجموعه ها باید عدد ۲ رو به توان تعداد عضوهای اون مجموعه برسونیم. در مورد مثال قبلی دیدیم که سه تا عضو داشت و ۸ تا زیرمجموعه نوشتیم. چون ۲ به توان ۳ مساوی ۸ میشه.
فرمول تعداد زیرمجموعه های ۲ عضوی از یک مجموعه n عضوی
برای بدست اوردن تعداد زیرمجموعه های ۲ عضوی از یک مجموعه که درکل n عضو داره باید از فرمول زیر استفاده کنیم:
تعداد زیرمجموعه های ۲عضوی=n×(n-1)÷۲
مثال: تعداد زیرمجموعه های دو عضوی در یک مجموعه ۱۰ عضوی چندتاست؟
جواب : طبق فرمول ۴۵ تا زیرمجموعه ۲ عضوی داره : ۴۵=۲÷۹۰=۲÷(۱-۱۰)×۱۰








عااالی متشکر
سپاس از شما
کوچکترین عضو اعداد حساب………… است
۰
صفر
مجموعه اعداد اول بین ۱و۶به صورت……. است
عدد «رادیکال سه» یک عدد……… است
هر یک از مجموعه های زیر را به صورت دیگر بنویسید؟
{۲و۱و۰و-۱}
میشه بی زحمت جوابشو بگین
مجموع اعداد اول بین یک و شش میشود {2و3و5}
عدد رادیکال 3 یک عدد گنگ است.
X|XEZ,-1<x<2 یعنی x هایی که x عضو (E) مجموعه اعداد صحیح (Z) است و x بین 1- و 2 قرار دارد.