یکی از روش های محاسبه ب م م یا همان بزرگترین مقسوم علیه مشترک دو عدد ، تجزیه آنها به روش درختی و نوشتن اعداد به صورت حاصلضرب شمارنده های اول است. این جمله رو به خاطر بسپارید : ب م م برابر است با حاصلضرب شمارنده های اول مشترک با کمترین تکرار. اما این جمله یعنی چی و چطوری میشه از ….
محاسبه ب م م یا بزرگترین مقسوم علیه مشترک به روش تجزیه درختی
یکی از روش های محاسبه ب م م یا همان بزرگترین مقسوم علیه مشترک دو عدد ، تجزیه آنها به روش درختی و نوشتن اعداد به صورت حاصلضرب شمارنده های اول است. در درس تجزیه عدد به شمارنده های اول به روش تجزیه درختی یاد گرفتیم که چطوری میشه به روش درختی عددها رو تجزیه کرد. در مورد محاسبه ب م م جمله زیر رو به خاطر بسپارید :
ب م م برابر است با حاصلضرب شمارنده های اول مشترک با کمترین تکرار
خب شمارنده های اول یک عدد رو از کجا باید پیدا کنیم؟؟؟ بله از راه تجزیه عدد
با یه مثال درس رو توضیح میدم براتون.
مثال : ب.م.م دو عدد ۱۸۰ و ۴۸ را پیدا کنید.
ابتدا باید اعداد ۱۸۰ و ۴۸ رو تجزیه کنیم:
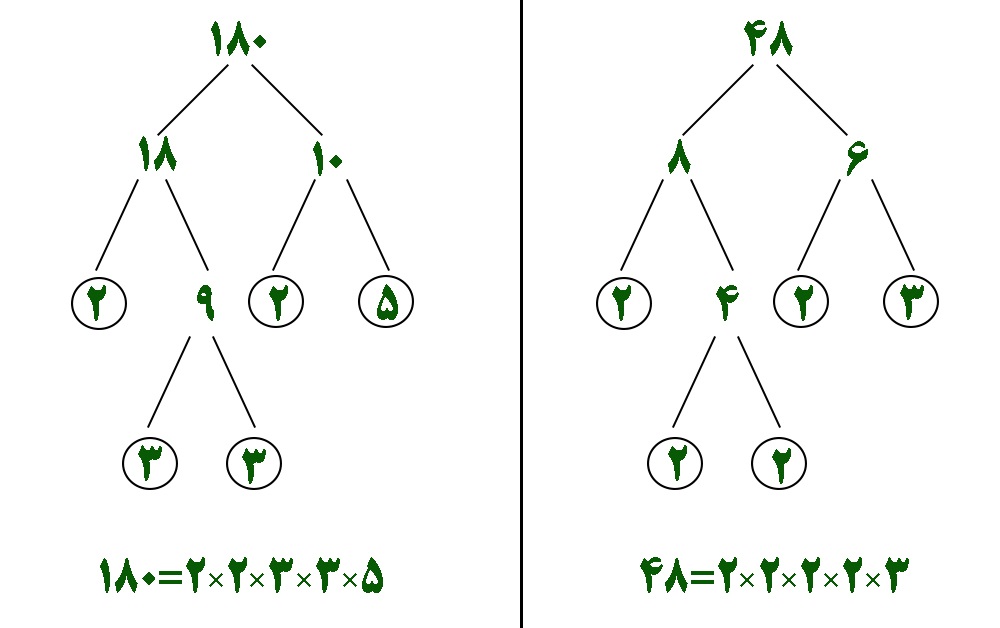
پس از تجزیه این عددها می تونیم اون ها رو به صورت حاصلضرب شمارنده های اولشون به صورت زیر بنویسیم:
۱۸۰=۲ × ۲ × ۳ × ۳ × ۵
۴۸=۲ × ۲ × ۲ × ۲ × ۳
حالا چیزایی که هم توی ۱۸۰ هستند و هم توی ۴۸ هستند رو مشخص می کنیم. ما اینجا اونا رو یک رنگ کردیم ولی شما میتونید دورشون خط بکشید.
۱۸۰=۲ × ۲ × ۳ × ۳ × ۵
۴۸=۲ × ۲ × ۲ × ۲ × ۳
یک ۲ از بالا رو با یک ۲ از پایین، قرمز کردیم.
یک ۲ از بالا رو با یک ۲ از پایین، بنفش کردیم.
عدد بالایی دیگه ۲ نداره، پس کارمون با ۲ تموم شد میریم سراغ ۳
یک ۳ از بالا رو با یک ۳ از پایین نارنجی کردیم.
چون عدد پایینی دیگه ۳ نداره، پس کارمون با ۳ هم تموم شد میریم سراغ ۵
پایینی اصلا ۵ نداره، پس کاری به کار ۵ هم نداریم.
حالا فقط کافیه عددهای رنگی رو درهم ضرب کنیم تا ب م م بدست بیاد.
۱۲ = ۳×۲×۲ = ب م م دو عدد ۱۸۰ و ۴۸
دیدید چه آسون بود !
پس به صورت خلاصه میگم اول هر دو عدد رو تجزیه میکنیم، عددهای مثل هم رو در هم ضرب میکنیم.
آهاااااا……… راستی یادم رفت که بگم ب م م دو عدد رو با گذاشتن پرانتز دور عددا نشون میدن. مثلا :
(۴۲ و ۱۰) یعنی ب م م دو عدد ۱۰ و ۴۲
اینجا ممکنه بپرسید خب عددهای دیگه ای که باقی مونده به چه درد می خوردن!؟ اون عددها برای محاسبه ک م م استفاده خواهند شد. اگر محاسبه ک م م رو هم دوست دارید ببینید، روی لینک زیر کلیک کنید:
ک م م یا کوچکترین مضرب مشترک به روش تجزیه درختی اعداد
چندتا مثال دیگه میزنم براتون :
با استفاده از روش تجزیه ب م م اعداد داده شده را بدست آورید.
الف – ( ۳۰ و ۵۰ )
پاسخ الف :
ابتدا اعداد را به صورت درختی تجزیه میکنیم :
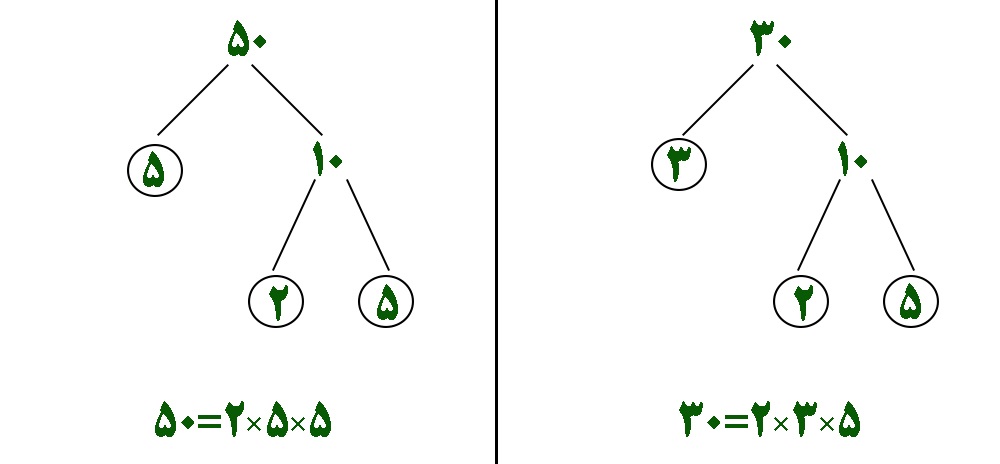
الان میتونیم اعداد ۳۰ و ۵۰ رو به صورت حاصلضرب شمارنده های اول بنویسیم :
۵۰ = ۲ × ۵ × ۵
۳۰ = ۲ × ۳ × ۵
یک دونه ۲ و یک دونه ۵ توی این دوتا عدد مثل هم هستش. اینا رو در هم ضرب می کنیم.
( ۵۰ , ۳۰ ) = ۲ × ۵ = ۱۰
ب – ( ۴۴۱ و ۱۴۷ )
پاسخ ب :
ابتدا اعداد را به صورت درختی تجزیه میکنیم :
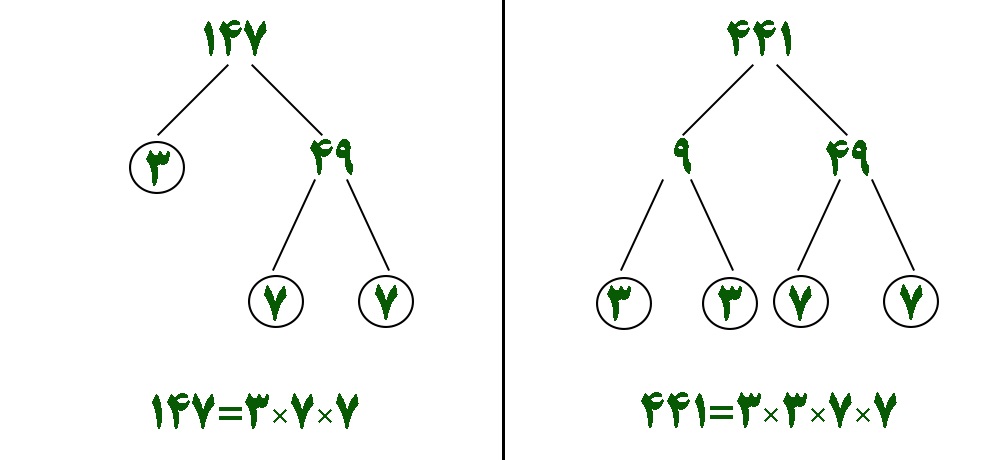
الان میتونیم اعداد ۴۴۱ و ۱۴۷ رو به صورت حاصلضرب شمارنده های اول بنویسیم :
۱۴۷ = ۳ × ۷ × ۷
۴۴۱ = ۳ × ۳ × ۷ × ۷
یک دونه ۳ و دوتا ۷ توی ۴۴۱ و ۱۴۷ مثل هم هست. اینا رو درهم ضرب می کنیم:
( ۱۴۷ , ۴۴۱ ) = ۳ × ۷ × ۷= ۱۴۷
نکته ۱ :
زمانی که پس از تجزیه دو عدد هیچ شمارنده مشترکی بین دو عدد مشاهده نمیشه یعنی بزرگترین شمارنده مشترک دو عدد مساوی با یک است. مثال : ۵۰ و ۲۱ رو در نظر بگیرید:
۵۰ = ۲ × ۵ × ۵
۲۱ = ۳ × ۷
چون هیچی مشترک ندارند، ب م م آنها مساوی با ۱ است.
نکته ۲ : ب م م هر عدد و یک مساوی با یک است.
مثال : ۱=(۳۰ و ۱)
نکته ۳ : ب م م هر دو عدد اول مساوی با یک است.
مثال : ۱=(۵ و ۷)
نکته ۵ : ب م م هر دو عدد متوالی (پشت سر هم) مساوی با یک است.
مثال : ۱=(۲۰ و ۲۱)
نکته ۶ : اگر عدد a بر عدد b بخش پذیر باشد، ب م م مساوی با عدد b یعنی عدد کوچکتر است.
مثال : ۶=(۶ و ۲۴)
تمرین : ب.م.م دو عدد ۱۲۰ و ۷۵ را بدست آورید. جوابتون رو میتونید توی بخش نظرات بذارید.








ایول
عالی
خیلی عالی بود ممنون 💯🙏
ممنون از نگاهتون
سلام تجزیه دو عدد ۱۲۰,۷۵ برابر است با:
۵×۳×۲×۲×۲×۲=۱۲۰
۵×۳×۳=۷۵
اعداد۳ و ۵ مشترک هستند
ب.م.م برابر است با:
۵ × ۳ = (۱۲۰٫۷۵)
سلام توی تجزیه ۱۲۰ ، یک دونه ۲ زیاد نوشتید ولی جواب ب.م.م درسته
سلام ببخشید میشه ک م م عدد های ۱۲،۱۶ رو هم توضیح بدید توش گیر کردم
خیلی ممنون بسیار عالی ،🙏🏻🙏🏻
سلام
پس از تجزیه دو عدد ۱۲۰،۷۵ برابر است با :
۲×۲×۳×۵×۲=۱۲۰
۳×۵×۵=۷۵
اعداد ۳ و ۵ در هر دو مشترک هستن پس ب.م.م برابر است با :
۱۵=۵×۳=(۷۵ ،۱۲۰)
بسیار عالی
سلام
پس از تجزیه دو عدد ۱۲۰ و ۷۵، برابر است با:
۳×۲×۵×۲×۲=۱۲۰
۳×۵×۵=۷۵
اعداد ۳ و ۵ در هر دو مشترکند، پس ب.م.م برابر است با:
۱۵=۳×۵=(۱۲۰,۷۵)
بسیارعالی
سلام
با این روش تجزیه درختی
ک م م عدد 9 و 12 رو نمیشه حساب کرد؟
باید چه کار کنیم؟
سلام با روش تجزیه حل میکنیم.
۹ میشه ۳×۳
۱۲ میشه ۲×۲×۳
عدد ۳ بین شون مشترک،باید تعداد بیشتره رو انتخاب کنیم. یعنی
۳×۳
حاصل ۳×۳ رو در همه غیرمشترک ها یعنی ۲×۲ باید ضرب کنیم.
جواب :
۳۶=۲×۲×۳×۳
سی و شش میشه باید مضرباشو نو بنویسی
چرااا نمیشه ؟؟ 😐