در دنباله حسابی هر جمله با اضافه شدن عددی ثابت به جمله قبلی بدست می آید. این عدد ثابت را قدر نسبت نامیده و با حرف d نشان …
پیدا کردن مقدار جملات و جمله عمومی در دنباله حسابی
در دنباله حسابی هر جمله با اضافه شدن عددی ثابت به جمله قبلی بدست می آید. این عدد ثابت را قدر نسبت نامیده و با حرف d نشان می دهند. جملات هر دنباله را با حرف انگلیسی و شماره آن جمله را در زیروند همان حرف نشان می دهند.
به طور مثال دنباله زیر ، یک دنباله حسابی به شمار می آید چون هر جمله با جمع شدن عدد ۷ با عدد قبلی بدست می آید.
۴ , ۱۱ , ۱۸ , ۲۵ , ۳۲ , ۳۹ , ۴۶ , ….
اگر چهار جمله اول آن را بخواهیم جداجدا نشان دهیم به صورت زیر در می آید:
![]()
دنباله حسابی در واقع یک دنباله خطی است که جمله عمومی آن را می توان به صورت زیر نشان داد:

بنابراین برای اینکه جمله عمومی یا جمله nام یک دنباله حسابی مشخص شود، کافی است جمله اول و قدر نسبت آن معلوم باشد.
——————————————–
مثال : جمله ۲۰ ام یک دنباله حسابی را بدست آورید به طوریکه جمله اول دنباله ۵ و قدر نسبت آن ۳ باشد.
جواب : به جای t1 عدد ۵ و به جای d عدد ۳ میذاریم. عدد ۳ باید در پرانتز قبلیش ضرب بشه و جوابش رو با ۵ ساده کنیم.
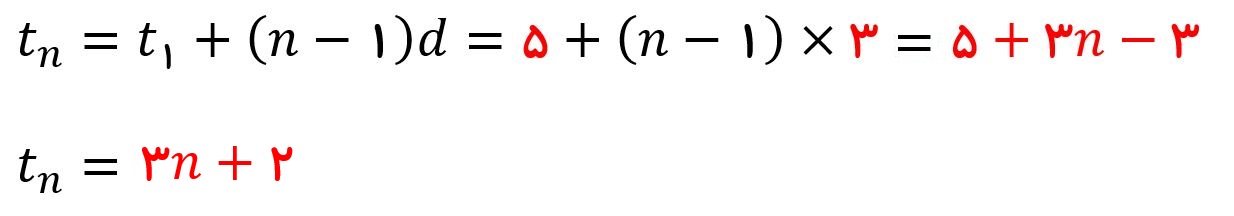
حالا که جمله nام این دنباله را داریم. برای بدست آوردن جمله ۲۰ ام فقط کافیه به جای n عدد ۲۰ قرار بدهیم.
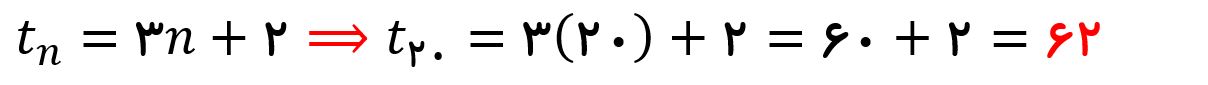
بنابراین جمله ۲۰ام این دنباله حسابی ۶۲ است.
—————————————————-
در بعضی مثال ها خودمان باید به طریقی جمله اول و قدر نسبت را مشخص کنیم.
مثال : در دنباله زیر جمله ۱۸ام را بدست آورید.
۱۷ , ۲۱ , ۲۵ , ۲۹ , ۳۳ , ۳۷ , …
جواب : همانطور که می بینید اولین جمله این دنباله ۱۷ است. اما از کجا قدر نسبت را بدست آوریم!؟ خیلی ساده اگر عدد هر جمله را منهای جمله قبلیش کنیم قدر نسبت بدست میاد . مثلا ۴= ۲۱-۲۵
پس جمله nام و جمله ۱۸ ام آن را مانند مثال قبل یادداشت می کنیم.
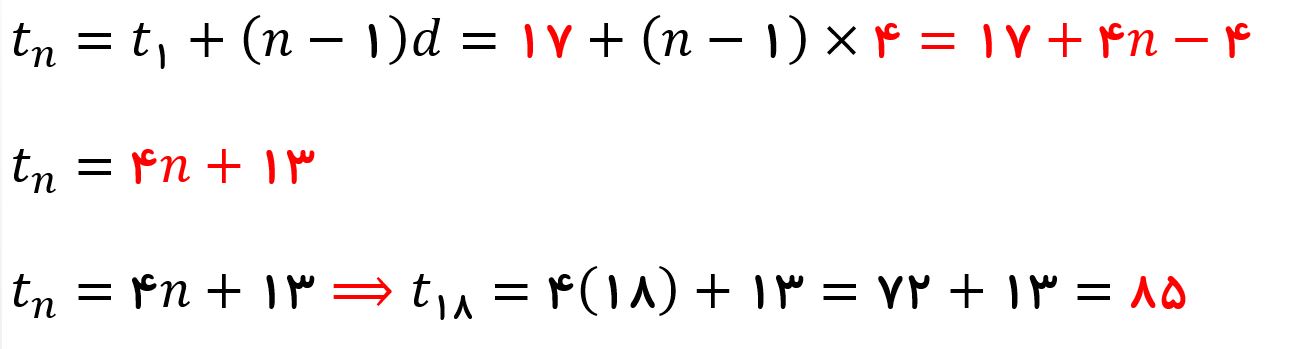
پس جمله ۱۸ ام این دنباله حسابی ۸۵ است.
———————————————–
در دنباله های حسابی می توانیم هر جمله برحسب جمله اول و قدر نسبت بنویسیم:
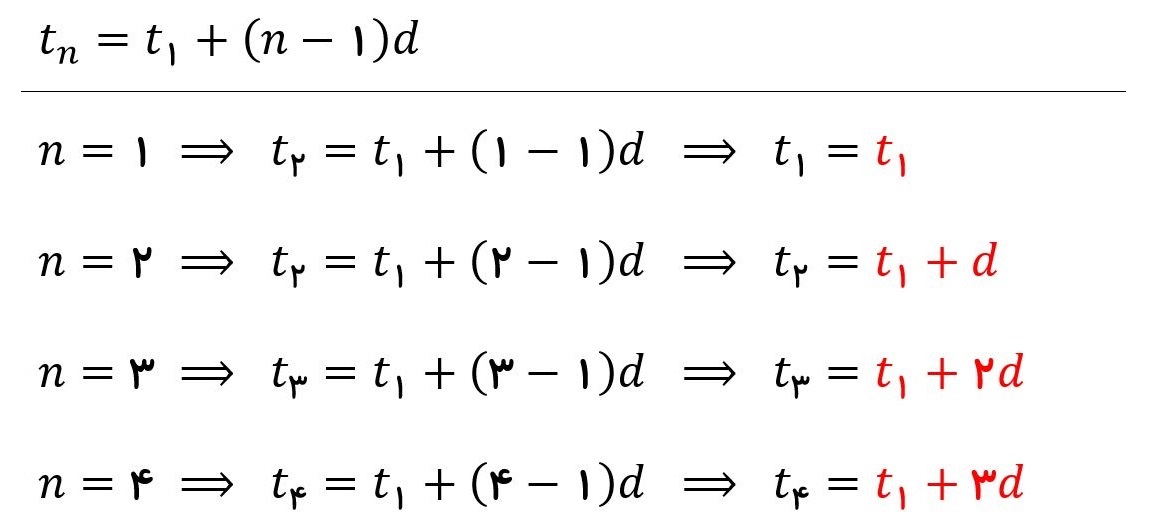
در دنباله حسابی هر جمله برابر است با t1 بعلاوه یک واحد کمتر از شماره خودش ضربدر d
از این خاصیت در حل خیلی از مسئله های مربوط به این درس می توان استفاده کرد.
مثال : اگر در یک دنباله حسابی جمله نهم مساوی با ۷۷ و جمله چهاردهم مساوی با ۱۲۲ باشد، قدر نسبت و جمله اول و جمله عمومی این دنباله را بدست آورید.
جواب : جمله نهم را به صورت ۷۷=t1+8d و جمله چهاردهم را به صورت ۱۲۲=t1+13d مینویسم. از تفریق این دو رابطه از هم و حل معادله مقدار d بدست می آید. بعد از آن مقدار d=9 را در معادله دوم قرار داده تا t1 بدست آید.
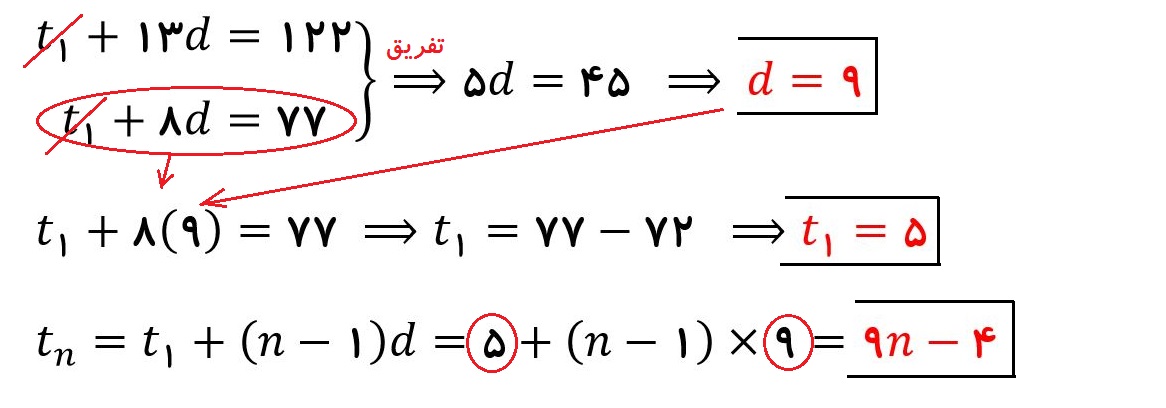










جمله عمومی دنباله حسابی an^3+2n^2+bn+c÷n+1 می باشد.اگر a6=17 باشد؛مقدار a+b+c را به دست آورید
جمله 0 + (قدرنسبتx ان)
عالی و پر کار برد
توی اون تیپ سوال ها ک میگفت دو جمله از یک دنباله رو داریم یه کاری هم میشد کرد اینکه:
۱:اختلاف جمله ها. t14-t9=5
۲:این عدد ضربدر dمیکنیم 5d
۳:اختلاف دو جمله را بدست میاریم:. 122-77=45
۴:معادله را تشکیل میدیم:. 5d=45
درنهایت داریم:. d=9
خوب بود((
سلام ببخشید تو سوال اخر از کجا فهمیدین که باید از طریق t1+8d=77 جمله اول رو بدست بیاریم
چرا ازt1+13d=122جمله اول رو بدست نیاوردیم?
🙏🏻
فرقی نمی کند
فرقی نمیکنه از هر دو تاشم میتونی بری
سلام لطفا این را جواب دهید:
سه عدد تشکیل دنباله حسابی می دهند، به طوریکه مجموع آنها ۹ و حاصل ضرب انها ۱۵ می باشند ان سخ عدد کدامند؟
سلام
5 , 3 , 1 ,
1 , 3 , 5
سلام لطفاaن=a1(n_1)*d
جمله بیستمو ب دست بیار؟
سلام ،،،، بسیار عالی بود ،،،،، و قابل درک ،،،،،،، سپاسگزارم لطفا در مورد واسطه هم توضیح بدین ،،،، بخصوص وقتی که جمله ها بیشتر از سه جمله هست ،،،، و تعداد جمله ها زوج هست ،،،،، بسیار سپاسگزارم
a4+a8=14
و
a9+a13=40
حالا گفته قدر نسبت رو به دست بیارید
۲.۶
بیست و شش پنجم
سلام ما یه سوالی داریم که گفتهa1+a4+a7+a12=160
جمله ششم چند است؟
البته من یازدهمما
اونارو جمع کنیم میشه 4a1+20d=160حالا اینو تقسیم بره 4 می کنیم میشه a1+5d=40جمله ششم هم میشه a6=a1+5d یکی ان دیگه .پس جمله ششم هم میشه 40
خیلی عالی بود
برای پیدا کردن دو جمله بین دوتا جمله دیگه در دنباله هندسی باید چکار کنیم؟
دو جمله داده شده را برهم تقسیم میکنیم و از جواب ریشه سوم میگیریم تا قدر نسبت بدست بیاد
مثلا بین ۴ و ۳۲ میخواهیم ۲ جمله دیگر هندسی بنویسیم
۳۲ تقسیم بر ۴ میشه ۸ و از ۸ ریشه سوم میگیریم جواب میشود ۲
یعنی قدر نسبت ما ۲ است. جمله اول ضربدر ۲ میشه ۸ و ۸ ضربدر ۲ میشه ۱۶ و ۱۶ ضربدر ۲ میشه ۳۲
نکته : همیشه ریشه رادیکال از تعداد اعدادی که میخواهیم یک واحد بیشتر است.
اگه دو جمله نا متوالی از یک دنباله حسابی رو بدن .
مثلا به ما جمله ۳۶ و ۱۲ از یک دنباله حسابی رو بدن . قدر نسبت برابر هست با
جمله سی شیشم منهای جمله دوازدهم تقسیم بر سی شش منهای دوازره
13d و 8d داخل مثال اخر از چه روشی ب دست اومد؟!
👍خوبه
توی مثال اخر میگیم جمله ۹ مساوی با ۷۷ اونd رو از کجا بدست اوردین؟
از فرمولی که برای پیدا کردن dاستفاده میشه که فرمولش اختلاف جملات تقسیم بر اختلاف شماره جملات هست در مثال بالا 45 =77-122که این میشه اختلاف جملات و 5=9-14و اینم میشه حاصل اختلاف شماره بعد از او 9=5÷45 که میشه 9=d
ظابطه دنباله را چگونه باید پیدا کرد؟
خیلی مفید
جمله عمومی2-،2،2- ،2 چیه
نوسانی
عالی😙
جمله عمومی میشه منفی یک که دنباله هندسی هستش
سلام پپاسخ این چی میشه به ترتیب شده ۱-۲-۵-۸ حالا میگه جمله یازدهم چیه
خیلی خوبه
دنباله حسابی هندسی قدر نسبت ۳،۱۰،۱۷،۲۴
عالی بود.
عالی بود