در این درس میخواهیم زاویه های خارجی در چند ضلعی های منتظم را معرفی کنیم. یک چند ضلعی محدب رو در نظر بگیرید. توی هر گوشه دوتا خط به هم میرسند تا یک زاویه بوجود بیاد. به اون خط ها …
زاویه خارجی چیه؟
در این درس میخواهیم زاویه های خارجی در چند ضلعی های منتظم را معرفی کنیم. یک چند ضلعی محدب رو در نظر بگیرید. توی هر گوشه دوتا خط به هم میرسند تا یک زاویه بوجود بیاد. به اون خط ها ضلع های زاویه گفته میشه. این زاویه که بین ضلع های زاویه تشکیل شده رو زاویه داخلی میگن که قبلا باهاش آشنا شدیم. حالا اگه یکی از ضلع های زاویه رو به صورت خط راست ادامه بدیم، زاویه ای که بین این امتداد و ضلع دیگه زاویه تشکیل میشه، زاویه خارجی گفته میشه. در شکل زاویه خارجی با رنگ آبی مشخص شده است.
رابطه بین زاویه داخلی و خارجی در هر گوشه
توی تعریف گفتیم که ضلع زاویه رو باید به صورت خط راست ادامه بدیم . اگه به شکل زیر دقت کنید کاملا واضح است که توی هر گوشه زاویه داخلی و خارجی مکمل هم هستن و یا به عبارتی :
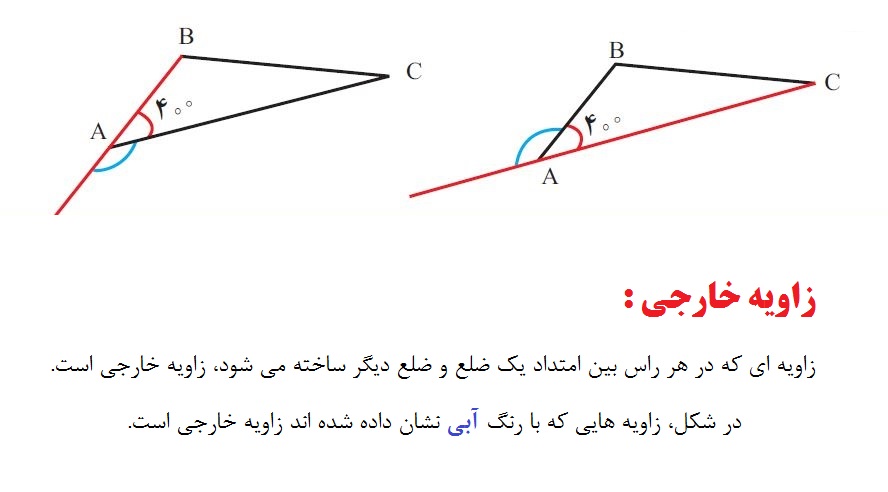
در هر گوشه جمع زاویه داخلی و خارجی مساوی ۱۸۰ است.
محاسبه زاویه های خارجی در چند ضلعی های منتظم
برای محاسبه زاویه های خارجی در چند ضلعی های منتظم یک تمرین خیلی عالی توی کتاب هست. با انجام دادن اون به یک نتیجه خیلی مهم میرسیم. الان میخوایم تمرین کتاب رو باهم حل کنیم و راجع بش بحث کنیم.
میدونیم اگه از تعداد اضلاع ۲ تا کم کنیم و جوابش رو در ۱۸۰ ضرب کنیم، مجموع زاویه های داخلی چند ضلعی منتظم بدست میاد.
میدونیم مجموع زاویه داخلی و خارجی در هر گوشه هم برابر ۱۸۰ میشه. پس مجموع زاویه های داخلی و خارجی کل شکل رو اگه بخوایم باید تعداد گوشه ها رو در ۱۸۰ ضرب کنیم.
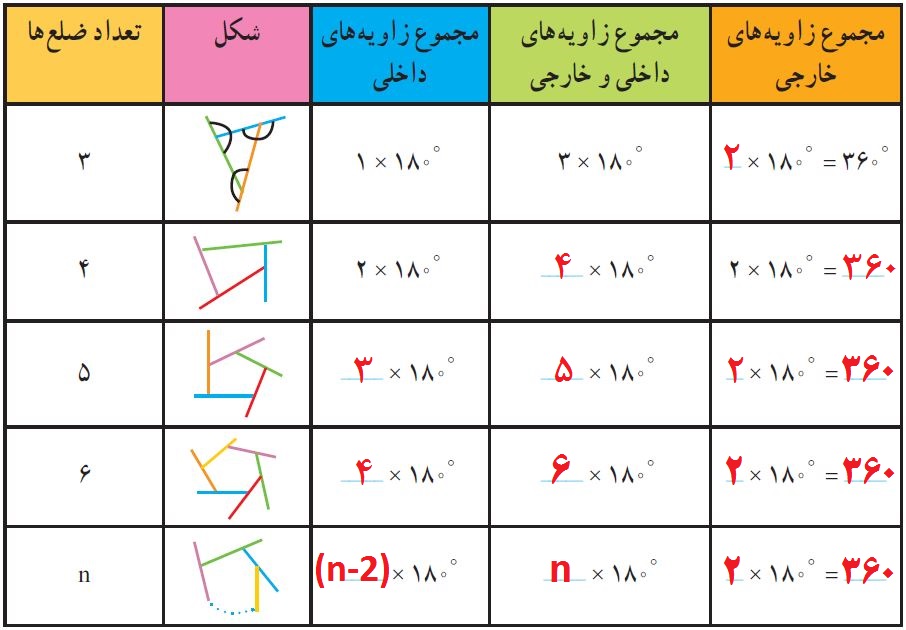
با دونستن این دو مورد ستوم سوم و چهارم جدول رو کامل میکنیم. حالا برای پرکردن ستون آخر باید ستوم سوم رو از ستون چهارم کم کنیم. اگه دقت کنید این اختلاف واسه همه شکل ها ۳۶۰=۱۸۰×۲ بدست اومده. از این تمرین نتیجه میگیریم که :
مجموع زاویه های خارجی همیشه مساوی ۳۶۰ است.
محاسبه هر زاویه خارجی یک چند ضلعی منتظم
در چند ضلعی های منتظم تمام ضلع ها با هم و تمام زاویه های هم با هم مساوی است. این مطلب برای زاویه های خارجی هم صادق است. یعنی تمام زاویه های خارجی هم باهم مساوی هستند. پس برای پیدا کردن اندازه هر زاویه خارجی در یک چند ضلعی منتظم به صورت زیر عمل می کنیم:
اندازه هر زاویه خارجی در چند ضلعی منتظم مساوی ۳۶۰ تقسیم بر تعداد اضلاع
البته میدونیم که تعداد اضلاع و تعداد زاویه ها باهم برابره !
اثبات اینکه چرا مجموع زاویه های خارجی هر nضلعی برابر ۳۶۰ میشه
در ابتدای درس گفتیم که در هر گوشه از یک چندضلعی جمع زاویه داخلی با زاویه خارجی مساوی با ۱۸۰ میشه. یک nضلعی دارای nگوشه است بنابراین جمع همه زاویه های داخلی با همه زاویه های خارجی مساوی با n×۱۸۰ هست. از طرفی میدونیم که جمع همه زاویه های داخلی به تنهایی از فرمول ۱۸۰×(n -2) بدست میاد. در نتیجه اگه فرمول اولی رو منهای دومی کنیم، عبارت باقی مونده برابر با مجموع همه زاویه های خارجی خواهد بود.
n×180 – (n-2)×180 = 180×n – n×180 + 2×180 = 180n – 180n + 360 = 360
به همین راحتی اثبات شد!







متوسط بود
خوب بود
سلام ببخشید
مجموع زاویه های داخلی ۱۲ ضلعی:
مجموع زاویه های خارجی ۱۲ضلعی :
اندازه یک زاویه خارجی 12 ضلعی :
اندازه یک زاویه خارجی ۱۲ ضلعی :
میشه بگین
مجموع زاویه های داخلی در هر nضلعی منتظم برابر است با : (تعداد اضلاع منهای 2) ضرب در 180 پس میشه :(2-12) *180= 1800 درجه.
مجموع زاویه های خارجی برای هر n ضلعی منتظم همیشه برابر 360 در جه است پس برای 12 ضلعی هم همان 360 درجه است.
هر زاویه خارجی در n ضلعی منتظم برابر است با 360 تقسیم بر n که برای 12 ضلعی داریم :360/12=30 درجه.
هر زاویه خارجی به علاوه هر زاویه داخلی میشه 180 درجه. زاویه دخلی را برای nضلعی بدست اوردیم 30 درجه . پس باید به این 30 درجه 150 درجه دیگر اضافه کنیم تا مجموع آن ها 180 درجه بشود.یا به عبارتی زاویه خارجی میشود 180 منهای زاویه داخلی. که میشه 30-180=150 درجه.
جواب ها به ترتیب از بالا به پایین میشه :
1800 درجه مجموع زاویه های داخلی
360 درجه مجموع زاویه های خارجی
30 درجه هر زاویه خارجی
150 درجه هر زاویه داخلی
نمیدونم
خب دیگه همه با همین فرمول بالا بدست میاد
خوب بود
عالی بود ممنونم از لطفتون 🙏🙏💓💖
جای خالی
دو خط عمود بر یک خط ………….هستند
چهار ضلعی منتظم ……………نام دارد
اندازه هر زاویه یک ۸ ضلعی منتظم……………..درجه است
قرینه معکوس عدد منفی ۲ویک پنجم میشه عدد………… .
اولی میشه موازی آخری هم میشه 5 دهم
😘😘😘
میشه جوابمو بدین لطفا خیلی نیاز دارم
3÷(6-7)6-6-
جوابش -4 میشه؟
6- بر سه تقسیم میشه حاصل میشه 2-
مقدار عبارت داخل پارانتز میشه 1-
پس 2- در 1- ضرب میشه حاصل میشه 2
2+ با 6- جمع میشه میشه 4-
ارههههه
اره
4میشه
در کدام چند ضلعی منتظم مجموع زاویه های داخلی سه برابر مجموع زاویه های خارجی است
مجموع زاویه های داخلی از رابطه زیر بدست می آید.
180(n-3)
مجموع زاویه های خارجی همیشه 360 است. که سه برابرش میشه 1080
فرمول اولی را باید مساوی با ۱۰۸۰ قرار داد.
جواب معادله n=9 بدست می آید.
مطالب خوبی بود ممنون
خوب بود. ممنون.
بله ممنون
بله