برای یک خط و یک دایره ، در حالتی که خط دایره را فقط در یک نقطه قطع می کند، می گوییم خط بر دایره مماس است. خط مماس در نقطه تماس بر ….
خط مماس بر دایره و ویژگی های آن
برای یک خط و یک دایره سه حالت ممکن است پیش بیاید:
1) خط، دایره را قطع نکند. در این حالت شعاع دایره کوچکتر از فاصله خط تا مرکز دایره است.
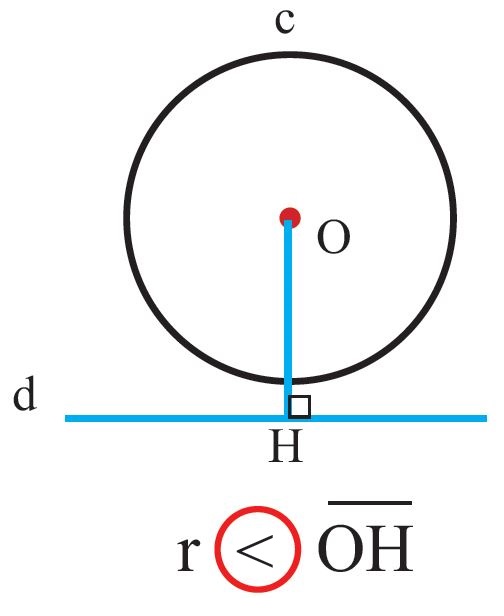
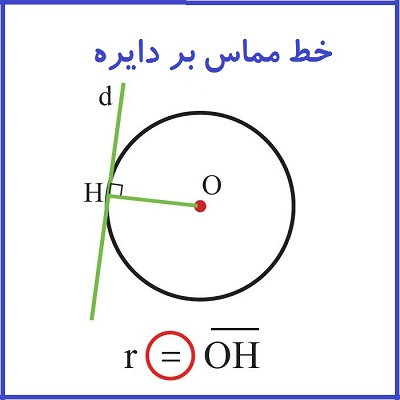
2) خط، دایره را در فقط در یک نقطه کند. در این حالت شعاع دایره مساوی با فاصله خط تا مرکز دایره است. در این حالت گفته می شود d خط مماس بر دایره است.
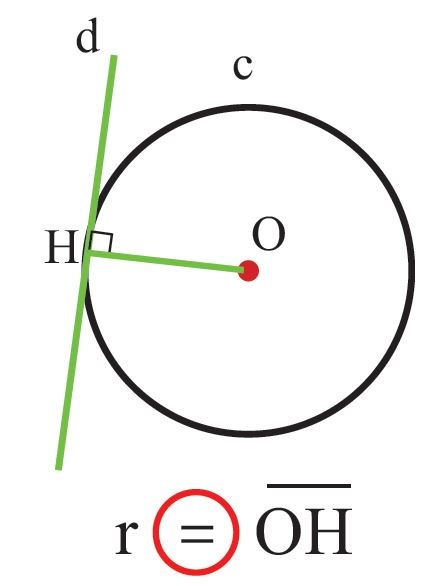
3 ) خط، دایره را در 2 نقطه قطع کند. در این حالت شعاع دایره بزرگتر از فاصله خط تا مرکز دایره است.
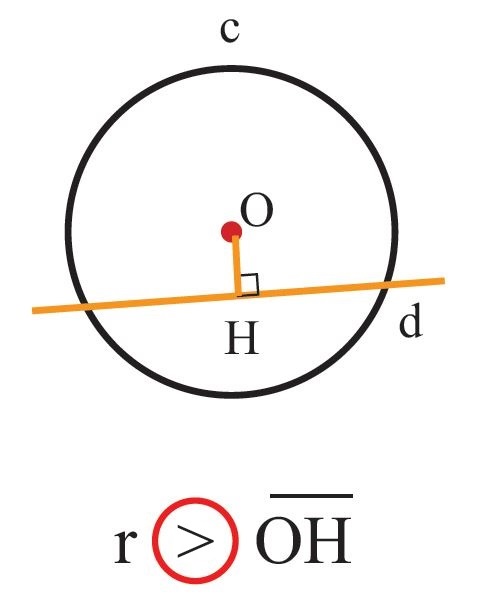
عمود بودن خط مماس بر شعاع دایره در نقطه تماس
همانطور که گفتیم، در حالتی که خط دایره را فقط در یک نقطه قطع می کند، می گوییم خط بر دایره مماس است.
ویژگی مهم خط مماس این است که خط مماس بر شعاع دایره در نقطه تماس ، عمود است.
در شکل زیر ، پاره خط AQ دایره را در یک نقطه قطع کرده و بر شعاع عمود است. پس AQ مماس بر دایره است.
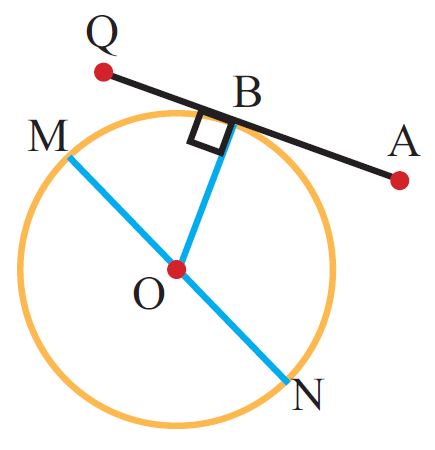
با استفاده از ویژگی عمود بودن خط مماس بر دایره ، می توان زاویه مجهول در مثلث های زیر را بدست آورید.
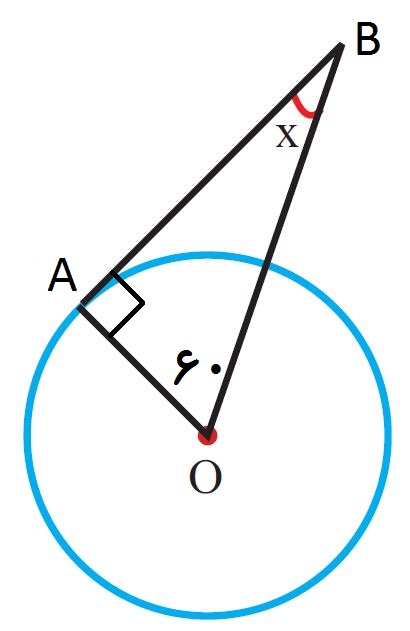
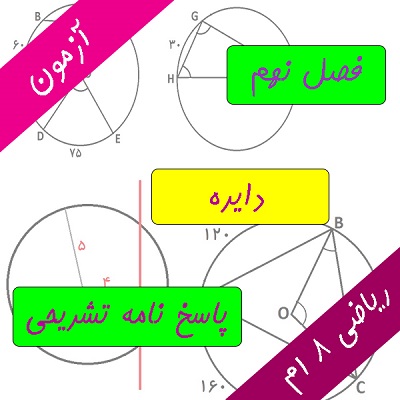
در مثلث زیر ، AB خط مماس بر دایره است. پس زاویه A=90 است.
از طرفی ، مجموع زاویه های A و B و O برابر 180 درجه و O=60 است. پس زاویه مجهول B برابر است با:
B=180-(90+60)=180-150=30
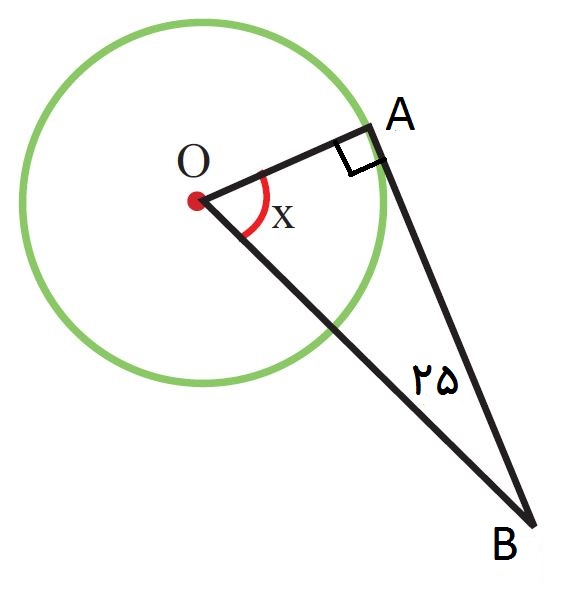
در مثلث زیر ، AB خط مماس بر دایره است. پس زاویه A=90 است.
از طرفی ، مجموع زاویه های A و B و O برابر 180 درجه و B=25 است. پس زاویه مجهول O برابر است با:
O=180-(90+25)=180-115=65
با استفاده از خاصیت عمود بودن خط مماس ، می توان به کمک رابطه فیثاغورس ، اندازه ضلع مجهول در مثلث را بدست آورید.
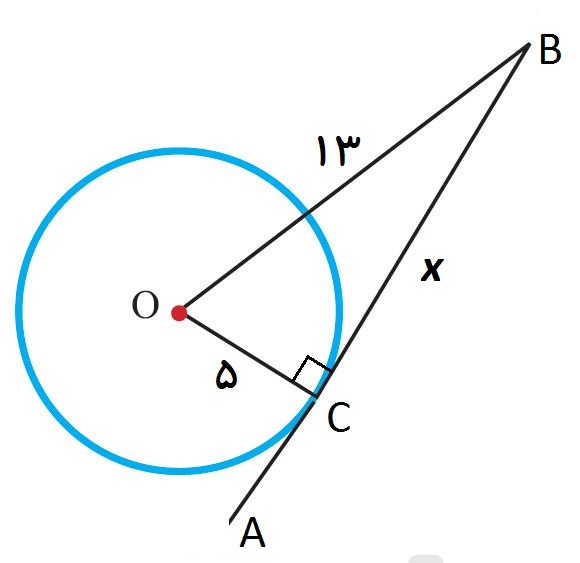
در مثلث زیر ، AB خط مماس بر دایره است. پس زاویه C=90 و پاره خط OB وتر مثلث است.
پاره خط OB وتر است. اندازه آن را به توان 2 می رسانیم، می شود 169
پاره خط OC ضلع قائمه است. اندازه آن را به توان 2 می رسانیم ، می شود 25
این دو عدد را منها کرده و عدد بدست آمده را می بریم زیر رادیکال تا پاره BC بدست آید.
BC=√(169-25)=√144=12
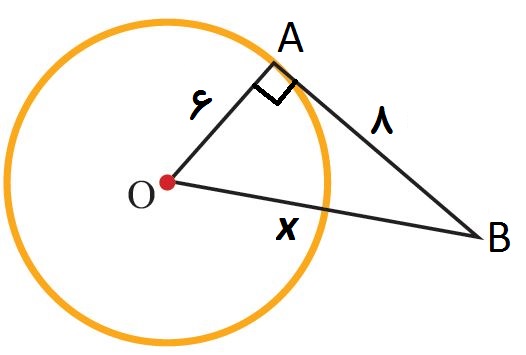
در مثلث زیر ، AB خط مماس بر دایره است. پس زاویه A=90 و پاره خط OB وتر مثلث است.
پاره خط OA ضلع قائمه است. اندازه آن را به توان 2 می رسانیم ، می شود 36
پاره خط AB ضلع قائمه است. اندازه آن را به توان 2 می رسانیم ، می شود 64
این دو عدد را جمع کرده و عدد بدست آمده را زیر رادیکال می بریم تا پاره OB وتر مثلث بدست آید.
OB=√(36+64)=√100=10
در این درس با خط مماس بر دایره آشنا شدیم و کاربردهای آن را در بدست آوردن زاویه و ضلع مجهول یاد گرفتیم.
- احتمال سکه و تاس و بررسی همه حالت های ممکن در احتمال
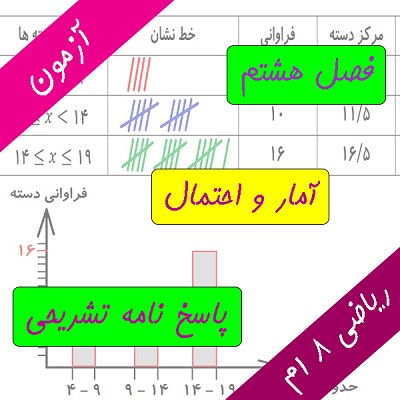
- جدول فراوانی داده ها ، تعاریف و نکات مربوط به آن
- تبدیل رادیکال به ضرب عدد در رادیکال چگونه انجام می شود؟
- نمایش اعداد رادیکالی روی محور اعداد به کمک مثلث قائم الزاویه
- تقسیم اعداد توان دار با پایه های مساوی یا با توان های مساوی
- به توان رساندن یک عدد توان دار داخل پرانتز چگونه است؟
- نمونه سوال های فصل به فصل







عالیبودکمکمکرد
عالی
با سلام و عرض ادب
از زحماتتان ممنونم. از تصویر پاره خط های مماس بر دایره استفاده کردم.
بی نهایت سپاس
سپاس از نگاهتون
توضیح مماس
خط مماس بر دایره ، خطی است که دایره را فقط در یک نقطه قطع می کند و در همان نقطه بر شعاع دایره عمود است.
سلام
مفید بودن👌🏻
بسیار عالی
بسیا عالی
آره
سلام خیلی عالی توضیح داده شده بود
سپاس
سلام کاملا ساده و قابل فهم بود
ممنون
خیلی عالی بود توضیحات کاملان حوبی داشت
عالی بودن
فوق العاده فصیح بود ممنون از زحمات شما
خیلی خوب توضیح دادین ممنونم.
عالی بود واقعا ممنون
بسیار عالی
سلام روزتون بخیر چرا اینا جواب نداره
سلام خسته نباشید چرا نمونه سوال دانلود نمیشه؟
سلام کدوم نمونه سوال؟
عالی بود ،❤️