یکی از چیزهای که همون ابتدای فصل سوم کتاب ریاضی هفتم باهاش آشنا میشیم، الگوهای عددی هستن. همون جوری که از اسمشون مشخصه، الگوی عددی یعنی یه سری عدد داریم که طبق یک الگوی مشخصی تکرار میشن. ما باید بلد باشیم که جمله nام الگوی عددی رو بدست بیاریم. معمولا توی سوالات از ما میخوان…
چطوری جمله nام الگوی عددی رو بدست بیاریم؟
یکی از چیزهای که همون ابتدای فصل سوم کتاب ریاضی هفتم باهاش آشنا میشیم، الگوهای عددی هستن. همون جوری که از اسمشون مشخصه، الگوی عددی یعنی یه سری عدد داریم که طبق یک الگوی مشخصی تکرار میشن. ما باید بلد باشیم که جمله nام الگوی عددی رو بدست بیاریم. معمولا توی سوالات از ما میخوان که طبق الگو پیش بریم و چند جمله بعدی رو خودمون بنویسیم. بذارید یه مثال ساده بزنم:
۲ , ۴ , ۶ , ۸ , …?… , …?… , …?…
به اعداد بالا توجه کنید. کاملا مشخص میشه که عددها دارن ۲ تا ۲ تا زیاد میشن. پس اگه بخوایم طبق همین الگو پیش بریم باید توی جاهای خالی به ترتیب ۱۰ و ۱۲ و ۱۴ بنویسم.
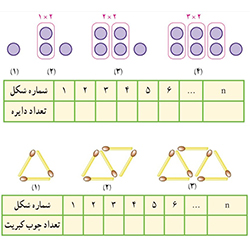
این که هرکدوم ازین عددها جمله چندم الگوی ما هستن، فقط نیاز داره که شمردن بلد باشیم!!! عدد ۲ جمله اول ، عدد ۴ جمله دوم ، عدد ۶ جمله سوم و الی آخر. این مساله به این آسونی رو چرا گفتم!؟ واسه اینکه به شما بگم جمله nام یعنی چی. به شکل زیر دقت کنید:
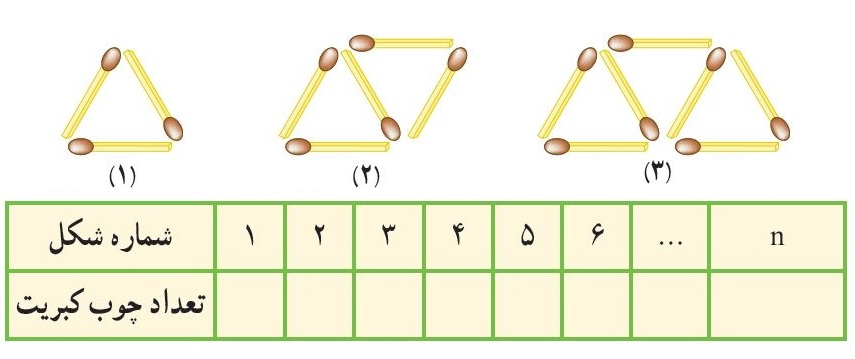
سه تا شکل اول الگو رو که خودش کشیده و به راحتی میتونیم بشماریم که هرکدوم چندتا چوب کبریت داره و توی جدول بنویسم. اما اگه از ما بخوان که مثلا بگیم شکل ۱۰۰ ام چندتا چوب کبریت داره، مسلما ما بیکار نیستیم که بیام شکل بکشیم و بعدش بشماریم! تازه اگه درست شکلش رو بکشیم. خب پس چیکار کنیم !؟ اینجاست که ما باید یه رابطه ریاضی بر اساس شماره شکل بدست بیاریم که تا بهش گفتیم تعداد چوب کبریت های شکل ۱۰۰ام رو میخوایم ، خیلی سریع به ما بگه چندتاست. به اون رابطه ی ریاضی میگن، جمله nام الگوی عددی .
حالا بیایم جمله nام تعداد چوب کبریت ها رو بدست بیاریم. اولین کارمون اینه که تعداد چوب کبریت هایی که توی همین سه تا شکل میبینیم بشماریم و جدولش رو کامل کنیم:

خب حالا مشخص میشه که تعداد چوب کبریت ها داره ۲ تا ۲ تا زیاد میشه. بنابراین شکل چهارم ۹ تا ، شکل پنجم ۱۱ تا ، شکل ششم ۱۳ تا و …. تا میرسیم به شکل nام . واسه شکل nام باید همون رابطه ی ریاضی که بهتون گفتم رو بدست بیاریم. با این روشی که میخوام به شما یاد بدم توی ۹۰درصد مساله ها به راحتی میتونید جمله nام رو بدست بیارید. اما اون روش چیه ؟؟؟
روش بدست آوردن جمله nام الگوی عددی
اگه یک الگوی عددی داشته باشم که هر عدد اون با یک مقدار ثابتی جمع میشه و عدد بعدی بدست میاد، میتونیم از فرمول زیر استفاده کنیم:
(مقدار ثابت − جمله اول) + n × مقدار ثابت = جمله nام
مثلا برای مسئله چوب کبریت ها عددها ۲ تا ۲ تا زیاد میشه، پس یعنی اون مقدار ثابت عدد ۲ هست. اگه جمله اول (یعنی ۳) رو منهای ۲ کنیم جواب ، ۱ میشه. پس جمله nام میشه : ۲n+1
الان که جمله nام رو بدست آوردیم، اگه بخوایم بفهمیم شکل ۱۰۰ام چندتا چوب کبریت داره فقط کافیه مقدار n رو ۱۰۰ بذاریم:
۲۰۱ = ۱ + ۱۰۰ × ۲ = تعداد چوب کبریت شکل ۱۰۰ام
چندتا مثال دیگه میزنم تا این مساله رو به خوبی یاد بگیرین.
مثال : در الگوهای عددی زیر جمله nام را بدست آوردید.
۲ , ۴ , ۶ , ۸ , ….
عددها ۲ تا ۲ تا زیاد میشن و جمله اول (۲) منهای مقدار ثابت (۲) مساوی صفر میشه.
پس جمله nام : ۲n
۳ , ۶ , ۹ , ۱۲ , ….
عددها ۳ تا ۳ تا زیاد میشن و جمله اول (۳) منهای مقدار ثابت (۳) مساوی صفر میشه.
پس جمله nام : ۳n
۶ , ۱۰ , ۱۴ , ۱۸ , ….
عددها ۴ تا ۴ تا زیاد میشن و جمله اول (۶) منهای مقدار ثابت (۴) مساوی ۲+ میشه.
پس جمله nام : ۲+۴n
۳ , ۸ , ۱۳ , ۱۸ , ….
عددها ۵ تا ۵ تا زیاد میشن و جمله اول (۳) منهای مقدار ثابت (۵) مساوی ۲- میشه.
پس جمله nام : ۲−۵n
۱ , ۸ , ۱۵ , ۲۲ , ….
عددها ۷ تا ۷ تا زیاد میشن و جمله اول (۱) منهای مقدار ثابت (۷) مساوی ۶- میشه.
پس جمله nام : ۶−۷n
چندتا الگو که حتما باید بلد باشید!
الگوی اعداد ۰ و ۲ و ۶ و ۱۲ و ۲۰ و … به صورت (n(n-1 است. چون این اعداد رو میتونیم به صورت زیر بازنویسی کنیم:
۰×۱=۰
۱×۲=۲
۲×۳=۶
۳×۴=۱۲
۴×۵=۲۰
اگه همین اعداد بالایی از ۲ شروع شده باشن یعنی به صورت ۲ و ۶ و ۱۲ و ۲۰ و … باشن الگو به صورت (n(n+1 میشه
این دوتا رو خوب یاد بگیرید چون خیلی پرکاربرد هستن. بذارید یک مثال هم بزنیم
مثال : الگوی اعداد ۲ و ۴ و ۸ و ۱۴ و … را بدست آورید.
پاسخ : ابتدا این اعداد رو به صورت زیر بازنویسی می کنیم:
۲+۰=۲
۲+۲=۴
۲+۶=۸
۲+۱۲=۱۴
همانطور که ملاحظه می کنید الگوی ۰ و ۲ و ۶ و ۱۲ در این اعداد موجود است تنها با این تفاوت که بعلاوه ۲ هم شده. پس شما هم الگوی گفته شده رو باید با عدد ۲ جمع کنید. یعنی جواب به صورت ۲+(n(n-1 میشه. خیلی راحت!
جمله n ام الگوهای درجه دوم
یکی دیگه از الگوهایی که زیاد سوال میشه به صورت زیر هست:
۵ , ۸ , ۱۳ , ۲۰ , ۲۹ , …
به طریقه بدست اومدن اعداد در این الگو توجه کنید.
| … | ۲۹ | ۲۰ | ۱۳ | ۸ | ۵ |
| ↓ | ↓ | ↓ | ↓ | ↓ | ↓ |
| … | ۲۰+۹ | ۱۳+۷ | ۸+۵ | ۵+۳ | ۵ |
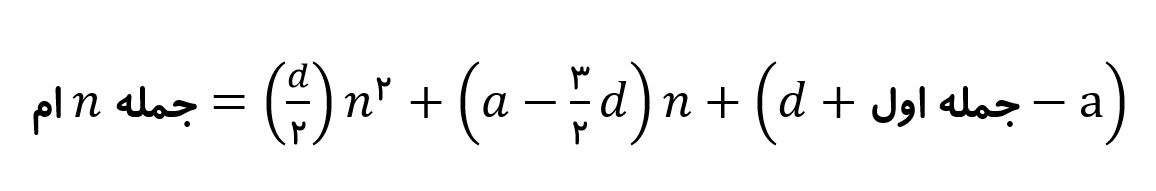
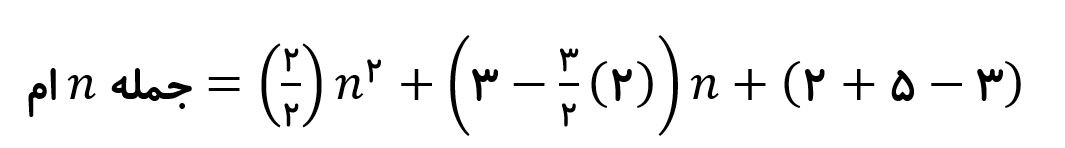
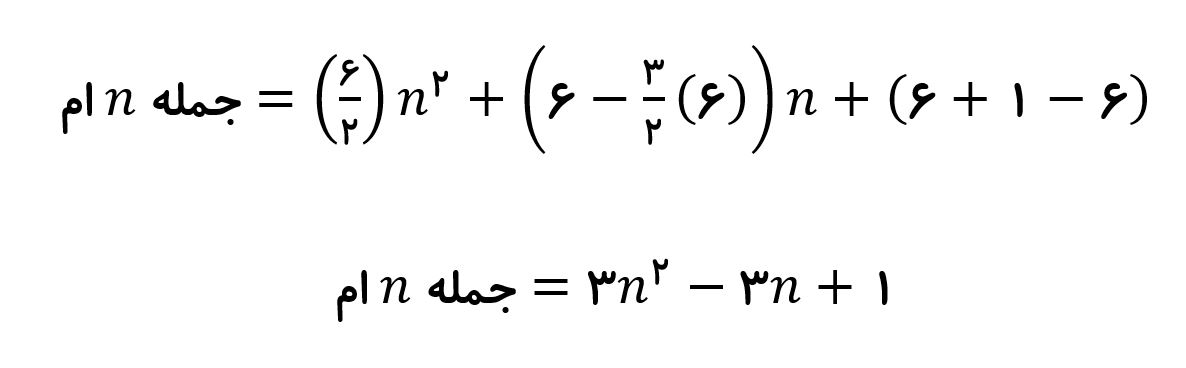








خودم فهمیدم متشکر🙏🙏
بسیار عالی
الگویی که بدست اوردید رو اینجا بنویسید تا بقیه دوستان هم استفاده کنند.
سلام الگو
۰,۱,۳,۴,۱۲,۱۳ رو میشه واسه من حل کنید با تشکر فراوان🙏🙏
سلام الگو
1,4,8,16 رو میشه واسه من حل کنید ممنون میشم
این الگو از جمله دوم به بعد از رابطه 2 به توان n پیروی میکند، اما جمله اول این الگو از این رابطه پیروی نمیکند، پس این دنباله جمله n ام ندارد
این دنباله در صورتی جمله n ام دارد که جملات آن به صورت 2,4,8,16 باشد که در این صورت جمله nام آن همان 2 به توان n است.
۳.۷.۱۰ جمله آن ام چیه؟
این الگو یک دنباله درجه دو است.
جمله n ام آن برابر با
i0/5*(-n^2+11n-4) =an
میباشد
۴n-۱
رابطه بین ۳،۶،۹،۱۰،۱۵ چییی میشههههه
اگر الگو به صورت 3و6و9و12و15و… باشد، یک دنباله حسابی را نشان میدهد که در آن قدر نسبت برابر با d=3 است و جمله اول هم برابر با a1=3 است. پس فرمول دنباله از رابطه an=a1+(n-1)d باید حساب شود. داریم:
an=3+(n-1)3
پس با ضرب کردن 3 داخل پارانتز و ساده کردن داریم:
an=3+3n-3=3n
پس فرمول جمله میشه:
an=3n
سلام
آیا برای این الگو میتوان جمله ی بعدی نوشت؟
3،8،30،132
سلام برای این الگو نمیتوان جمله بعدی نوشت، چون اعداد آن از الگوی ثابتی پیروی نمیکنند. مثلا دنباله حسابی یا هندسی یا درجه دو و… نیست.
سلام
۳ = ۳×۱
۸ = ۴×۲
۳۰ = ۶×۵
۱۳۲ = ۱۲×۱۱
مثل اینکه خیلی هم بی ربط نیستند به هم. از روی این الگو شاید بشه عدد بعدی رو حدس زد.
سلام ببخشید میشه عدد
ا،۳،۹
را به من جواب درحد چهارم ابتدایی بدید ممنون.
سلام جوابش میشه 3 به توان شماره هر جمله تقسیم بر 3. یعنی برای بدست آوردن هر جمله از دنباله، باید عدد 3 را به تعداد شماره جمله در خودش ضرب کنیم و حاصل رو تقسیم بر سه کنیم. مثلا عدد 9 که جمله سوم دنباله هست میشه:
3 ضرب در 3 ضرب در 3 تقسیم بر 3 که میشه همون 9. یا عدد 1 که جمله اول هست میشود، 3 تقسیم بر 3.
سلام بسیار کامل و خوب
جمله nام الگوی زیر رو میگین؟
۱,۲,۴,۸,۱۵
سلام جمله nام این الگو چی میشه؟
2،6،9،27،30،
سلام خسته نباشید
لطفا جمله nام اعداد
۱،۱۴،۱۷،۲۰
را بفرمایید
سلام. اگر الگو به صورت 11 و 14 و 17 و 20 باشد، میبینیم که هر جمله جدید با اضافه کردن سه واحد به جمله قبل درست شده است، یعنی 11+3=14 و 14+3=17 و… پس این دنباله یک دنباله حسابی با جمله اول 11 و قدر نسبت 3 است. جمله عمومی این دنباله هست : جمله اول + (شماره جمله مدر نظر منهای یک) در قدر نسبت.
an=a1+(n-1)*d
an=11+(n-1)*3
an=3n+8
۴.۶.۹
سلام خسته نباشید
میشه جمله nام این الگو رو بفرستین واسم بچا هرچقد حلش میکنم فرمولشو نمیتونم ب دست بیارم
1,4,9,16,25
سلام. فرمولش میشه شماره جمله به توان دو
سلام
میشه n ضربدر n یا همون n به توان ۲